Technical Note:
Measuring E-fields 25-1000 MHz with the NIST dipole-detector.
by Christopher Scott, W4NEQ
Much of the material was adapted from NIST technical note numbers 1309 and 1098. Thanks to Galen Koepke, Electronics Engineer, Fields & Interference Metrology Group, NIST, for helping me reproduce related calibration procedures.
There is often a requirement in RF and antenna work for gain standard antennas. Knowing the incident field strength in volts-per-meter present within the intrinsic 376.73 ohm impedance of free space within a subject volume of space can be useful as a gain reference, or used for power-density information.
Desirable gain-standard antenna qualities include stable and accurately known gain, a high degree of dimensional stability, and clearly defined polarization. Ease of reproduction is also a good thing. Before we delve too deeply into this experimental piece, note that it cannot distinguish between different frequencies.

Reflections notwithstanding, a thin half-wave dipole has a gain of 2.14 dB over a theoretical spherically radiating (isotropic) antenna. The dipole's doughnut shaped pattern yields this gain. The half-wave dipole is well accepted as a natural, reliably reproducible reference standard. Can it be used to measure incidental fields? Sure, assuming that it's matched to a balanced, well characterized transmission line run several wavelengths perpendicular to the dipole element to prevent induced currents.
Only then, can a calibrated receiver or detector accurately measure the antenna terminal voltage or power, after being adjusted for mismatch and line loss. This creates a difficult test environment and introduces unnecessary sources of error.

Worst case error and total uncertainty may be calculated simply as the sum of the percentages, or decibels. However since the sources of error are for the most part unrelated and independent, with each error unlikely to be at its extreme value and in the same direction, this approach is very conservative. A more realistic method is the root-sum-square calculation. Finding the rss uncertainty follows its name; square the components, sum those squares, take the square root. In any case the goal is to reduce or eliminate sources of error.
The antenna and detector described in this note represent the standard hardware used for measuring the calibrated E-field at the NIST open-field antenna test range. The worst case total uncertainty is one decibel, or using the rss method, .6 dB, according to NIST scientists.
The NIST standard receive antenna is a resonant, thin, half-wave dipole with a high impedance detector-voltmeter installed across the gap of the center insulating support, which is usually made of Teflon. The detector diode is a high-burnout Schottky microwave type. Hewlett-Packard is one manufacturer of these units. The Schottky diode has a low turn-on voltage and a high (70v) peak reverse voltage rating. This type of diode provides a very high shunt impedance (greater than one-hundred Meg ohms) for the signal levels used.

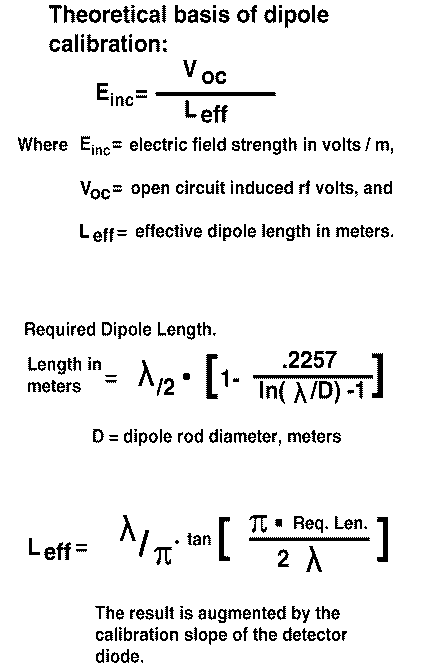
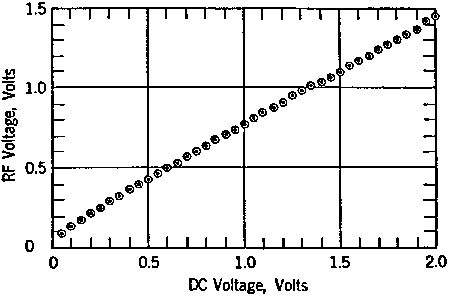
A center insulator with banana connectors installed in both ends is one way to allow for frequency change. Cut-to-length rods may then be used for various frequencies. Alternatively, telescoping whips may be installed, permitting quick adjustment over a wide range. The formula for calculating the proper length of the elements according to Schelkunoff's algorithm is shown. In the case of the telescoping whip elements, the equivalent diameter can be approximated by integrating diameter along their lengths. This is not extremely critical to accuracy, since a small reactive component in the source impedance remains negligible compared to the load resistance.
Note that in the presence of strong interfering signals, the dipole-detector system cannot be used for accurate measurements, due to the broadband detection. A noteworthy variation of this antenna is where the dipole length is adjusted to less than about one-ninth wavelength; instead of the current distribution being sinusoidal, it becomes triangular, and remains that way, extending the flat frequency response down to much lower frequencies.
Many broadband "isotropic" power density meters sum the output of three orthogonal dipoles like this to sense the E-field component. The effective length must of course, be calculated differently, due to the change in current distribution.
So exactly how many volts per meter is in that ether? Build the standard dipole-detector and know.